Here you can check 10th Class Geometry Questions with solution,Geometry Question Answers for grade 10th, Easy method to solve Geometry problems, Coordinate Geometry Questions Answer, Coordinate Geometry Exercise, Important geometry questions, 10th class geometry important questions with answer. If you have the query releated any questions of any other or this topic you can ask me easily to write below in comment section.
10th Pass Jobs - Click Here
10th Pass Jobs - Click Here
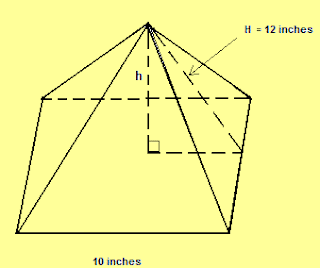
Q.1 Each side of square pyramid is shown below figures 10 inches. The
slant height, H, of this pyramid measures 12 inches.
.
a. What is the total surface area of
square inches, of the pyramid?
b. What is the area, in square inches, of
the base of the pyramid?
c. Using the height you determined in part
(c), what is the volume, in cubic inches, of the pyramid?
d. What is h, the height, in inches, of
the pyramid?
Answer
a) Total Surface Area is = 100 + 4*(1/2)*12*10 =
340 inches squared
b) Area of Square is 10* 10 + 100 inches squared
c) Volume of Pyramid is =
(1/3)*100*sqrt(119)
d) height is = sqrt(122 - 52) =
sqrt(119)
= 363.6 inches cubed
(approximated to 4 decimal digits)
Q. 2 The parallelogram shown
in the figure following has a perimeter of 44 cm and an area of 64 cm2. Find angle
T in degrees.
Answer
44 = 2(3x + 2) + 2(5x +
4) , solve for x
x = 2
height = area / base
= 64 / 14 = 32/7 cm
sin(T) = (32/7) / 8 =
32/56 = 4/7, T = arcsin(4/7) = 34.8 degree
Q. 3 Find the dimensions of a rectangle that has a length 3 meters more that its width & have a perimeter
equal in value to its area?
Answer
- Let Length be the L & W be the width of the
rectangle. L = W + 3
and Perimeter = 2L + 2W = 2(W + 3) + 2W = 4W + 6
Area = L W = (W + 3) W = W2 + 3 W
Area and perimeter are equal in value
Then W2 + 3 W = 4W + 6
Solve the above quadratic equation for W and substitute to find L
W = 3 and L = 6
Q. 4 Find
the area of the quadrilateral shown in the figure.(NOTE: figure not drawn to
scale)
Answer
ABD
is a right triangle then BD
2 =
152 + 152 = 450
Also
Sqart(BC) + Sqrt(CD) = 212 + 32 = 450
The
above means that triangle BCD is also a right triangle and the total area of
the quadrilateral is the sum of the areas of the two right triangles.
Area
of quadrilateral = (1/2)*15*15 + (1/2)*21*3 = 144



No comments:
Post a Comment